Maxwell has a chapter (no. XI) in volume II of his formative work A Treatise on Electricity and Magnetism entitled On energy and stress in the electromagnetic field. I suspect few people read the Treatise these days, just as few people read Newton's 'Principia', though Maxwell's work is full of insights. He writes the stress in long-winded form and succinctly in quaternion notation, another mathematical concept that needs background familiarity. He points out that stress in general has four consequences, which he quantifies. The first is a pressure in all directions (like that experienced below the surface of a liquid); the second is a directed tension (like stretched elastic - he gives more details); the third is a directed pressure (ditto); fourthly a couple tending to twist every element of the substance (ditto).

Near the close of the chapter he comments: In explaining the electromagnetic force by means of a state of stress in a medium, we are only following out the conception of Faraday, that the lines of magnetic force tend to shorten themselves, and that they repel each other when placed side by side. All that we have done is to express the value of the tension along the lines, and the pressure at right angles to them, in mathematical language, and to prove that the state of stress thus assumed to exist in the medium will actually produce the observed forces on the conductors which carry electric currents. ... We have merely shown that it is possible to conceive the mutual action of electric currents to depend on a particular kind of stress in the surrounding media, instead of being a direct and immediate action at a distance.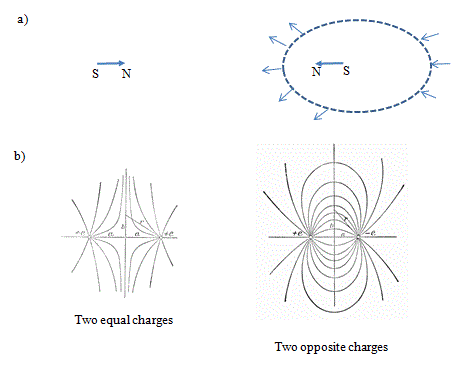

Diagrams illustrating the use of the Maxwell stress tensor

This gets to the heart of Maxwell's vision. A current is passed through a wire and deflects a compass needle some distance away. Is this 'action at a distance' of the current in the wire? Well if you want to think so, you can, said Maxwell, but you will have a lot of trouble both visualising this and getting the right answer. Maxwell's view is that the wire creates a field everywhere around it (obeying his equations) and the field is stressed. Indeed the field transmits the stress between interacting sources, charges or currents. It gets more interesting. Fig. a in the diagram to the right shows another example: two magnets. Consider an arbitrary surface enclosing one magnet. The force it experiences can be calculated by summing the stress over the surface. Maxwell showed that it doesn't matter what surface you choose, which is a powerful result. (For the mathematical, this comes about by a smart application of Gauss's theorem that converts volume integrals to surface integrals). You can select one surface close to the body or one further away. In practice, the surface of choice is the one for which the mathematics is easiest. Not only that, the problem has been reduced from a problem in electricity and magnetism to one in mechanics. In Maxwell's day, the top physicists were probably better versed in mechanics than they are today, so it was 'problem solved'.

Another implied feature of the Maxwell view is once the field is known we needn't know any information about its sources. In the everyday context of radio reception, we're all extremely familiar with the idea now. Our radio or mobile phone has no idea where the sources of vibrating charge are in the transmitting aerial, only the strength of the electromagnetic field in their vicinity. For historical reasons I've taken the next two images from the great 'Abraham and Becker'. This book, or at least an early incarnation of it authored by Abraham and Föppl, published in 1904, is the one Einstein praised for the insight it had given him. Max Becker may not have been that pleased for he had several public arguments with Einstein over Relativity, which he did not like. The book ran to at least 14 editions under the title Theorie der Elektrizitat and had a lifetime of over half a century. The first image shows field lines coming from two equal charges on either side of the origin. Choosing a surface that is a very large hemisphere (b in the diagram itself) around one charge, the stress everywhere on the surface is a pure pressure (until it fades away in the far distance off the plane shown). Adding it up over the hemisphere the result is just the force expected from Coulomb's law. It is always encouraging to see a general idea give the right answer in special cases. The second figure is the case of equal and opposite charges. In this case the stress is pure tension and upon adding it up the answer is correct.

In many engineering applications, the stress created by magnetic fields is more important than the electrical counterpart. In a non-magnetic medium it consists of a tensile stress of B²/2μ₀ along a line of force and a compressive stress of B²/2μ₀ in every direction at right angles to the line of force. This is the stress Maxwell was discussing in relation to Faraday's work. Likewise the electric field causes two stresses. If D is proportional to E then these are a tensile stress of DE/2 along the line of force at each point and a compressive stress of DE/2 in every direction at right angles to the line of force at each point.

So powerful was Maxwell's idea of mathematically derived fields permeating all space that fields became the reality of 20th century physics. Einstein introduced the gravitational field characterised by its stress-energy tensor. Today's particle physics recognises a number of short-range fields, like the Higgs field. The characteristic of all fields is that anything that interacts with it, interacts with the field around it, not its source.

References: James Clerk Maxwell, A Treatise on Electricity and Magnetism, 3rd ed'n, Clarendon Press, Oxford, 1892. The 3rd edition is the most likely edition to come across and has been reprinted on at least 4 occasions. The original is out of copyright and a digital version can be obtained from several web-sites. There are 2 volumes.

Max Abraham revised by Richard Becker The Classical Theory of Electricity and Magnetism, 2nd edition 1950 (translation of the 14th German edition of vol. 1 by John Dougall), Blackie & Son, Ltd., London and Glasgow.

JSR 2016