 |
Maxwell's Equations | Maxwell Legacy Concepts |
|---|
In a nutshell |
Nowadays we talk of a 'magnetic field' or an 'electric field' as if these ideas were obvious. It was Maxwell who gave substance to these terms. Before his time they had been just metaphors of Michael Faraday to represent the influence of sources of magnetism and electricity. Maxwell showed that these fields could be expressed mathematically by equations that describe their behaviour and interactions. He derived his equations from the known laws of electricity and magnetism, with some additional crucial insight of his own. Maxwell's equations have survived the revolutionary changes of 20th century physics and they underpin a huge range of natural phenomena. In particular they predict the possible existence of electromagnetic waves and how they behave, including light and radio waves. |
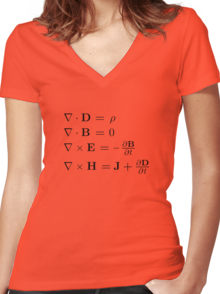 T-shirt advertising Maxwell's equations from www.redbubble.com |
|---|
| Technical detail | 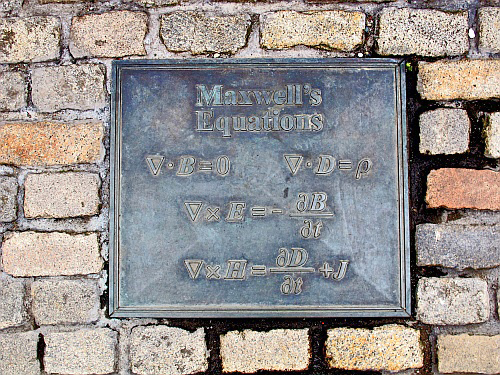
Maxwell's equations on a plaque beside his statue in George Street, Edinburgh Maxwell's equations date from the early 1860s but the elegant four lines that are usually quoted today use the vector notation introduced by Oliver Heaviside in the 1880s. E and D refer to different aspects of the electric field. The electric field is created by electric charge. H and B refer to different aspects of the magnetic field. Magnetic field is created by charges in motion. The 'nabla' symbol ∇ (like a point-down triangle) is used followed by a dot to represent a quantity called the 'divergence'. ∇× is the quantity known as 'curl'. This is a technical quantity relating to the effect of circulating around a closed loop in the field. The other field we are most familiar with, the Earth's gravitational field, has zero circulation so it's no help in seeing what's going on with 'curl'. In fluid flow, though, whirlpools and smoke rings have circulation and the circulation of air velocity is a key quantity in modern meteorology. Fields diverge when they have point sources. The first equation on the right (∇.B = 0) says there are no point sources of the magnetic field B. i.e. magnetic monopoles don't exist. To put it another way, magnetic field lines don't start or stop anywhere but form closed loops. The second equation (∇.D = ρ) says that charge is the source of the electric field D, ρ being the density of charge. Electric field lines start on positive charge and finish on negative charge. The third equation relates the curl of E to the rate of change of magnetic field (∇×E = - ∂B/∂t). This is the relationship underlying the workings of dynamos and transformers, to give two examples, where a changing magnetic field through a circuit induces an EMF in the circuit. It is why we have AC mains and not DC mains. The final equation defining ∇×H introduces the symbol J for the current density and includes the fact that a changing electric field will induce a magnetic field in the surroundings. Indeed current, which is moving electric charge, is the primary source of magnetic field. With these equations, Maxwell showed that in free space electric and magnetic fields obey a wave equation whose solution has the properties of light and radiant heat. One property of the solution is that in free space both the electric and magnetic fields are at right angles to the direction of propagation. This fitted exactly with the known polarisation properties of light. What clinched the association with light and heat for Maxwell was that the speed of propagation of electromagnetic waves was determined by constants known from purely electromagnetic experiments. They predicted a value for the speed of electromagnetic waves that within experimental error matched the measured speed of light. His prediction kick started refined experiments to measure the speed of light accurately (notably by Leon Foucault) and he himself undertook a very careful electromagnetic experiment to measure the electromagnetic constants more accurately. The net result of this experimental activity over several years confirmed Maxwell's prediction of electromagnetic waves travelling at the speed of light. When materials are involved, Maxwell's equations written so succinctly need to be unpacked. The relationship between D and E implies the concept of dielectric constant and that between B and H magnetic permeability. Other concepts need to be created such as capacitance, inductance and conductivity. Developments are needed such as the force on a moving charge (the Lorentz force) and the energy associated with the electromagnetic field (the Poynting vector). With these and appropriate numerical values in particular cases then a huge range of phenomena of the electromagnetic field can be teased out: Ohm's law, why glass is transparent but silver reflects, how to design directional radio and TV aerials, how to make microwave ovens and wifi networks, how to generate electricity efficiently from mechanical motion, how to accelerate particles to sufficiently high energy that new medical imaging techniques can be developed, and hundreds more insightful applications that couldn't be done before Maxwell came along. In practice, handling Maxwell's equations is not that easy for a clear head is needed, a range of interconnected concepts must be kept in mind at once and a good degree of applied mathematical skill is desirable. As a result, courses on electricity and magnetism are recognised to be amongst the hardest in university Physics and Engineering degrees. Maxwell himself was a master of all the attributes needed, able to develop the theory without being shown how by others. Fields fill all space and a given field defines an influence at any point in space. The electric field is a vector quantity defining the magnitude and direction of the force on a unit charge placed at the point. The magnetic field defines the torque on a miniscule magnet, which is why iron filings show up magnetic field lines and compasses work. Maxwell showed how to formulate a field theory mathematically and hence quantitatively. 20th century physics has taken Maxwell's concepts and seen them as the way forward in describing the fundamental processes in nature. Quantum Field Theory is one result, General Relativity another. Fields are the modern reality. Maxwell, well before anyone today was born, showed how field theories could be constructed. Reference: almost any book on electricity and magnetism will discus Maxwell's equations, possibly in a variant way from the above, but one reference unpicking Maxwell's seminal paper of 1865 in modern notation is Longair M., 2015 ‘...a paper ...I hold to be great guns’: a commentary on Maxwell (1865) ‘A dynamical theory of the electromagnetic field’. Phil. Trans. R. Soc. A373: 20140473. http://dx.doi.org/10.1098/rsta.2014.0473. JSR 2016 |
|---|---|