Maxwell's legacy: Maxwell Colour Triangle

	Maxwell Coil	Maxwell Legacy Concepts

In a nutshell	The Maxwell coil is not a 'great discovery' in the sense of several other of Maxwell's achievements. It is more of a passing curiosity. The very first electromagnetic phenomenon recognised as such was Oersted's discovery in 1820 that a current through a wire could deflect a compass needle. Over the following decades this effect was made the basis of the very successful current measuring instrument known as the 'galvanometer'. The current to be measured was sent through a coil at the centre of which was placed a small compass needle. Various schemes were devised for measuring the twist produced on the compass needle, one of which was to attach a small mirror to a suspension thread holding up the needle. A beam of light reflected from the mirror to a scale enabled very small movements to be measured. The accuracy of this device was impaired if the magnetic field produced by the coil was not uniform over the area swept out by the compass needle. This was the problem addressed by Maxwell in designing a coil that has a particularly uniform magnetic field near its centre. The accompanying illustration is Maxwell's own, showing a coil in three parts at the centre of which hangs a small magnet with a mirror attached. The problem Maxwell's coil aims to solve is to design a coil with a uniform field over a substantial area near its centre. He comments in passing that if a coil were wound over a sphere, the field could be made uniform throughout the volume inside but that such a coil forms a closed surface, so that its interior is inaccessible. The Maxwell coil is a compromise, sufficiently good that at the centre a range of perturbing factors are all zero. The three parts can be imagined on the surface of a sphere. Maxwell describes the sizes, separations and relative number of turns necessary to achieve exceptional uniformity of magnetic field at the centre. There are other situations where a particularly uniform field is needed and Maxwell's solution could be used. Galvanometers, though, developed towards the end of the 19th century with a design that inverted the arrangement of magnetic field and coil. The coil was made very small and allowed to rotate on its axis inside a permanent magnetic field supplied by a surrounding magnet. These devices could be made robust and portable. They became the basis of the 'multimeter' for a century, before themselves being superseded by digital technology.	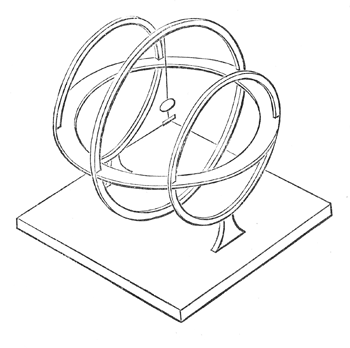Maxwell's version of a coil for producing a near uniform field at its centre.

Technical detail	The magnetic field along the axis of a circular coil of radius 'a' at a distance 'x' from its centre varies as na²/(x² + a²)^3/2, where n is the number of turns. The field falls away from the centre at an increasing rate until at x = a/2 there is a point of inflection where the rate of fall is steady before decreasing more slowly. Maxwell's good friend Hermann von Helmholtz realised that a working approximation to a constant magnetic field could be made by placing two identical thin coils parallel to each other a distance apart equal to their radius. The centre point between them would be at a distance a/2 from each coil and the rate of fall of two fields would cancel, leaving not only the first derivative of the field zero but also the second derivative (and indeed all even derivatives). The net result is shown in the first graph to the right. Maxwell's coil involves a central coil of radius a with two side coils each of radius (4/7)^0.5a placed on either side of the main coil at distance (3/7)^0.5a. The side coils have 49/64 turns compared with the main coil. The result is impressively good, as seen from the graph below right. Whereas the field from the Helmholtz coil has dropped by more than 1% at a distance 0.1a from the centre, Maxwell's coil is still within 1% at a distance of 0.4a. Helmholtz's coils are easier to make and set up so they have been the ones generally employed when a nearly uniform field is needed. Maxwell's coil could well be exploited more than it has been. For example a Maxwell coil only one quarter of the radius of a Helmholtz coil (one sixteenth of its area) will give a slightly better uniformity of field around its centre than the Helmholtz coil. Reference: Maxwell discusses his coil and Helmholtz's coil in articles 713 -715, pp 356 - 359 of James Clerk Maxwell, A Treatise on Electricity and Magnetism, vol. II, 3rd ed'n, Clarendon Press, Oxford, 1892. JSR 2016	The red and blue curves show the magnetic field produced by the individual coils of Helmholtz along their axis; the green curve is the total field from the two coils, illustrating the region of near constant field in the centre.
The green, blue and red curves show the magnetic field produced by the 3 parts of the Maxwell coil along the coil axis. The top dark-blue/purple curve is the total magnetic field.

Technical detail

The magnetic field along the axis of a circular coil of radius 'a' at a distance 'x' from its centre varies as na²/(x² + a²)^3/2, where n is the number of turns. The field falls away from the centre at an increasing rate until at x = a/2 there is a point of inflection where the rate of fall is steady before decreasing more slowly.

Maxwell's good friend Hermann von Helmholtz realised that a working approximation to a constant magnetic field could be made by placing two identical thin coils parallel to each other a distance apart equal to their radius. The centre point between them would be at a distance a/2 from each coil and the rate of fall of two fields would cancel, leaving not only the first derivative of the field zero but also the second derivative (and indeed all even derivatives). The net result is shown in the first graph to the right.

Maxwell's coil involves a central coil of radius a with two side coils each of radius (4/7)^0.5a placed on either side of the main coil at distance (3/7)^0.5a. The side coils have 49/64 turns compared with the main coil. The result is impressively good, as seen from the graph below right. Whereas the field from the Helmholtz coil has dropped by more than 1% at a distance 0.1a from the centre, Maxwell's coil is still within 1% at a distance of 0.4a. Helmholtz's coils are easier to make and set up so they have been the ones generally employed when a nearly uniform field is needed. Maxwell's coil could well be exploited more than it has been. For example a Maxwell coil only one quarter of the radius of a Helmholtz coil (one sixteenth of its area) will give a slightly better uniformity of field around its centre than the Helmholtz coil.

Reference: Maxwell discusses his coil and Helmholtz's coil in articles 713 -715, pp 356 - 359 of James Clerk Maxwell, A Treatise on Electricity and Magnetism, vol. II, 3rd ed'n, Clarendon Press, Oxford, 1892.

JSR 2016

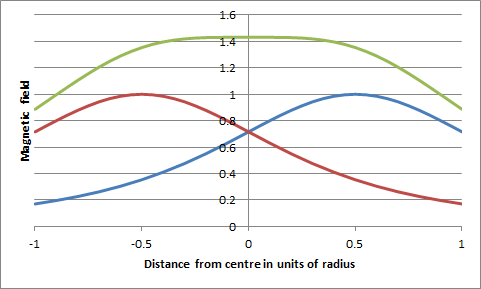The red and blue curves show the magnetic field produced by the individual coils of Helmholtz along their axis; the green curve is the total field from the two coils, illustrating the region of near constant field in the centre.

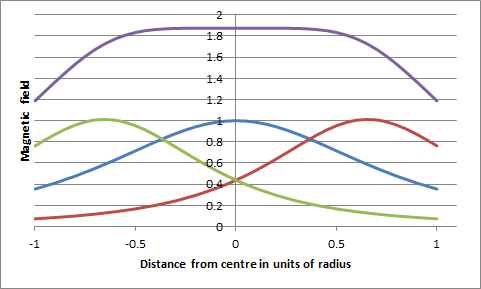The green, blue and red curves show the magnetic field produced by the 3 parts of the Maxwell coil along the coil axis. The top dark-blue/purple curve is the total magnetic field.