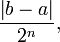Bisection method
From Wikipedia, the free encyclopedia
In mathematics, the bisection method is a root-finding algorithm which repeatedly divides an interval in half and then selects the subinterval in which a root exists.
Suppose we want to solve the equation f(x) = 0. Given two points a and b such that f(a) and f(b) have opposite signs, we know by the intermediate value theorem that f must have at least one root in the interval [a, b] as long as f is continuous on this interval. The bisection method divides the interval in two by computing c = (a+b) / 2. There are now two possibilities: either f(a) and f(c) have opposite signs, or f(c) and f(b) have opposite signs. The bisection algorithm is then applied recursively to the sub-interval where the sign change occurs.
The bisection method is less efficient than Newton's method but is not prone to the same odd behavior.
Contents |
[edit] Analysis
If f is a continuous function
on the interval [a, b] and f(a)f(b)
< 0, then the bisection method converges to a root of
f. In fact, the absolute error is
halved at each step. Thus, the method converges linearly,
which is quite slow.We can find the asymptotic error constant is 1/2. This is
because  .On
the other aspect, since the absolute error of bisection convergence is
.On
the other aspect, since the absolute error of bisection convergence is 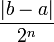 ,
the rate of convergence is
,
the rate of convergence is  which means the decrease of error is exponential. This means the convergence
speed actually is not so bad.On the positive side, the method is guaranteed to
converge if f(a) and f(b) have different signs.
which means the decrease of error is exponential. This means the convergence
speed actually is not so bad.On the positive side, the method is guaranteed to
converge if f(a) and f(b) have different signs.
The bisection method gives only a range where the root exists, rather than a single estimate for the root's location. Without using any other information, the best estimate for the location of the root is the midpoint of the range. In that case, the absolute error after n steps is at most
If either endpoint of the interval is used, then the maximum absolute error is
the entire length of the interval.
If f has several roots in the interval [a, b], then the bisection method finds the odd-numbered roots with equal, non-zero probability and the even-numbered roots with zero probability. More precisely, suppose that f has 2k + 1 simple roots x1 < x2 < … < x2k+1 in the interval [a, b] (the number of roots is odd because f(a) and f(b) have opposite signs). Assume that the roots are distributed independently and uniformly in this interval. Then, the probability that the bisection method converges to the root xi with i = 1, 2, …, 2k + 1 is zero if i is even and 1 / (k + 1) if i is odd (Corliss 1977).
[edit] Pseudo-code
Here is a representation of the bisection method in Visual Basic code. The variables left and right correspond to a and b above. The initial left and right must be chosen so that f(left) and f(right) are of opposite sign (they 'bracket' a root). The variable epsilon specifies how precise the result will be.
'Bisection Method
'Start loop
Do While (abs(right - left) > 2*epsilon)
'Calculate midpoint of domain
midpoint = (right + left) / 2
'Find f(midpoint)
If ((f(left) * f(midpoint)) > 0) Then
'Throw away left half
left = midpoint
Else
'Throw away right half
right = midpoint
End If
Loop
Return (right + left) / 2
[edit] See also
- Binary search algorithm
- Lehmer-Schur algorithm, generalization of the bisection method in the complex plane
[edit] References
- Burden, Richard L. & Faires, J. Douglas (2000), Numerical Analysis (7th ed.), Brooks/Cole, ISBN 978-0-534-38216-2 .
- Corliss, George (1977), "Which root does the bisection algorithm find?", SIAM Review 19(2): 325–327, ISSN 1095-7200 .
[edit] External links
- Bisection Method on Mathcad Application Server.
- Bisection Method Notes, PPT, Mathcad, Maple, Matlab, Mathematica from Holistic Numerical Methods Institute
- Module for the Bisection Method by John H. Mathews
- Java Code for Bisection Method by Behzad Torkian
- True example of using bisection method in computer programming free program to isoelectric point calculation
![A few steps of the bisection method applied over the starting range [a1;b1]. The bigger red dot is the root of the function.](Wikipedia, the free encyclopedia_files/250px-Bisection_method.png)