Physics header

Fourier Analysis of a Periodic Function

This applet is designed to demonstrate features of the real and imaginary components in the Fourier series of a periodic function. The Fourier expansion of a real function ƒ(t) may be written:

Fourier series.

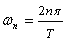Each component is specified by its amplitude, An, angular frequency ωn and phase φn. If ƒ(t) has period T then omega (for n = 0, ω0=0, φ0=0, A0=ƒ(t)). The display shows the coefficients of the eiωnt and e-iωnt terms namely:
C+ωn = Aneiφn = Ancos(φn)+isin(φn)
and C-ωn = Ane-iφn = Ancos(φn)-isin(φn)

The 'real' Fourier series graph shows the real parts of the coefficients and the 'imaginary' Fourier series graph shows the imaginary parts. The 'real' graph is even since the coefficients of eiωnt and e-iωnt are the same (Acos(φ)). The 'imaginary' graph is odd since the coefficients of eiωnt and e-iωnt have opposite signs.

The interactive capability shows the effect on the Fourier spectrum of changing the position of the time origin and also of varying ƒ(t) (by moving the t-axis vertically).

Adjusting the phase angles (φn): This is done by dragging the wave horizontally with the left mouse button

The phase angles φn depend on where the origin is located. If it is taken in the centre of a pulse (for the square wave) or a trough, ƒ(t) is then an even function f(t)=f(-t) and all the φn are zero; so the Fourier components are purely real.
If the time origin is on a rising or falling edge for a duty cycle of 50% then ƒ(t) is an odd function f(t)=-f(t) and the Fourier components are purely imaginary.
Dragging the origin makes no difference to the amplitudes An, as seen in the amplitude spectrum.

Adjusting the 'DC' term (ƒ(t)):

The term for ω=0 is purely real and equal to ƒ(t). Dragging the t-axis vertically with the right mouse button affects only the value of the Fourier component at t=0.

As in the previous applet the duty cycle and number of terms displayed can be altered on the panel.

Physics virtual library