
 |
Maxwell Bridge | Maxwell Legacy Concepts |
|---|
In a nutshell |
'Bridge' circuits are a highly desirable means of electrical measurement, for they are examples of 'null measurements'. In these, the unknown is compared with a multiple of a standard until no difference is detected. [Equivalently, a multiple of the unknown may be compared with the standard until no difference is detected. The inverse of the multiple then gives the value sought]. The Maxwell bridge (sometimes called the Maxwell L/C bridge) is a means of measuring electrical inductance. It was a passing idea among hundreds of innovations outlined in Maxwell's great Treatise on Electricity and Magnetism (section 778 in the 3rd edition), though you will be hard pressed to find any reference to this in modern texts on electrical measurement. The idea has proved fruitful and is now referenced in many electrical engineering courses and books. A range of commercial example bridges can be purchased that allow exploration of the practicalities of the Maxwell Bridge. There are also digital simulations. The Maxwell Bridge is based on the well-known Wheatstone's Bridge for measuring resistance that has a resistor in each of its four 'arms'. The Maxwell Bridge replaces one resistor by a coil, that can be considered as a resistance and inductance in series. Another arm has added to it a known capacitor. When balanced for amplitude and phase both the resistance of the coil and its inductance can be calculated. |
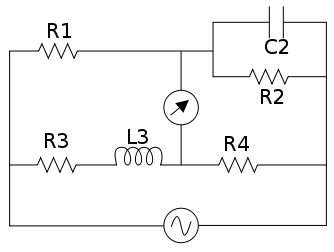 |
|---|---|---|
| Maxwell Bridge courtesy Wikipedia. R3-L3 is the inductor to be measured, C2 is a known (variable) capacitor that can be varied to balance the bridge using AC |
| Technical detail | In Maxwell's original description, the bridge was first balanced using a battery, as with a standard Wheatstone bridge. This determines the unknown resistance R3 since R3 = R1.R4/R2. Maxwell and his contemporaries didn't generally have access to a sinusoidal AC signal generator so had to resort to making and breaking the battery circuit and adjusting the variable capacitor so that the meter (a ballistic galvanometer) showed no flicker when this was done. Maxwell then calculated the inductance L3 = R1.R4.C2. These same balance conditions appear in a modern analysis that sets both the real and imaginary parts of the meter current (or oscilloscope voltage if an oscilloscope is used to show the bridge balance) to zero. Consider R1 and C2 as the variables. Neither balance condition depends on the frequency of the bridge, which is why Maxwell's original idea of making and breaking the circuit worked. There are some other practical issues, so the Maxwell bridge tends to be used at audio freqencies. In that case the detector can be (high impedance) earphones or, with some amplification, a loudspeaker. You might ask why an unknown inductance isn't balanced against a known inductance? Theoretically, you can. Maxwell devised a bridge for this, known as the Maxwell inductance bridge. It is similar to a Wheatstone bridge except two arms contain inductors (with accompanying resistances). Practically, standard inductors are less easy to make than standard capacitors. Secondly, inductors are more likely ot interact with each other via 'mutual inductance', throwing off the simple analysis of the bridge and adding an unknown to the measurement. However the Maxwell L/C Bridge can be used to determine capacitance, given a known inductance. Maxwell did devise other bridges. Although he was not a practising electrician (unlike his contemporaries Fleeming Jenkin and William Thomson) Maxwell knew more about the behaviour of electrical circuits than most professionals. He was particularly interested in establishing electrical standards and methods of accurate measurement. In 1887 Aytron and Perry devised their Secohmmeter, a device to be used in conjunction with Maxwell's bridges. It consists of two counter-rotating commutators, one in the battery circuit to generate (square wave) AC from the battery and the other to rectify the balance current. References: James Clerk Maxwell, A Treatise on Electricity and Magnetism, 3rd ed'n, Clarendon Press, Oxford, 1892. See pp 425-427 of Vol. II. B. Hague Alternating Current Bridge Methods, Isaac Pitman & Sons, London, 1938, includes over 20 pages discussing the use and development of Maxwell's bridge. JSR 2016 |
|---|